Cari Blog Ini

Jumat, 21 Januari 2011

stems Chaos theory Complex analysis

Foundations and philosophy

In order to clarify the foundations of mathematics, the fields of mathematical logic and set theory were developed. Mathematical logic includes the mathematical study of logic and the applications of formal logic to other areas of mathematics; set theory is the branch of mathematics that studies sets or collections of objects. Category theory, which deals in an abstract way with mathematical structures and relationships between them, is still in development. The phrase "crisis of foundations" describes the search for a rigorous foundation for mathematics that took place from approximately 1900 to 1930.[32] Some disagreement about the foundations of mathematics continues to present day. The crisis of foundations was stimulated by a number of controversies at the time, including the controversy over Cantor's set theory and the Brouwer-Hilbert controversy.
Mathematical logic is concerned with setting mathematics within a rigorous axiomatic framework, and studying the implications of such a framework. As such, it is home to Gödel's incompleteness theorems which (informally) imply that any formal system that contains basic arithmetic, if sound (meaning that all theorems that can be proven are true), is necessarily incomplete (meaning that there are true theorems which cannot be proved in that system). Whatever finite collection of number-theoretical axioms is taken as a foundation, Gödel showed how to construct a formal statement that is a true number-theoretical fact, but which does not follow from those axioms. Therefore no formal system is a complete axiomatization of full number theory.[citation needed] Modern logic is divided into recursion theory, model theory, and proof theory, and is closely linked to theoretical computer science.
p \Rightarrow q \, Venn A intersect B.svg Commutative diagram for morphism.svg
Mathematical logic Set theory Category theory

Theoretical computer science

Theoretical computer science includes computability theory, computational complexity theory, and information theory. Computability theory examines the limitations of various theoretical models of the computer, including the most powerful known model – the Turing machine. Complexity theory is the study of tractability by computer; some problems, although theoretically solvable by computer, are so expensive in terms of time or space that solving them is likely to remain practically unfeasible, even with rapid advance of computer hardware. A famous problem is the "P=NP?" problem, one of the Millennium Prize Problems.[33] Finally, information theory is concerned with the amount of data that can be stored on a given medium, and hence deals with concepts such as compression and entropy.
DFAexample.svg Caesar3.svg
Theory of computation Cryptography

Applied mathematics

Applied mathematics considers the use of abstract mathematical tools in solving concrete problems in the sciences, business, and other areas.
Applied mathematics has significant overlap with the discipline of statistics, whose theory is formulated mathematically, especially with probability theory. Statisticians (working as part of a research project) "create data that makes sense" with random sampling and with randomized experiments; the design of a statistical sample or experiment specifies the analysis of the data (before the data be available). When reconsidering data from experiments and samples or when analyzing data from observational studies, statisticians "make sense of the data" using the art of modelling and the theory of inference – with model selection and estimation; the estimated models and consequential predictions should be tested on new data.[34]
Computational mathematics proposes and studies methods for solving mathematical problems that are typically too large for human numerical capacity. Numerical analysis studies methods for problems in analysis using ideas of functional analysis and techniques of approximation theory; numerical analysis includes the study of approximation and discretization broadly with special concern for rounding errors. Other areas of computational mathematics include computer algebra and symbolic computation.
Gravitation space source.png BernoullisLawDerivationDiagram.svg Composite trapezoidal rule illustration small.svg Maximum boxed.png Two red dice 01.svg Oldfaithful3.png
Mathematical physics Fluid dynamics Numerical analysis Optimization Probability theory Statistics
Market Data Index NYA on 20050726 202628 UTC.png Arbitrary-gametree-solved.svg Signal transduction v1.png Ch4-structure.png GDP PPP Per Capita IMF 2008.png Simple feedback control loop2.png
Mathematical finance Game theory Mathematical biology Mathematical chemistry Mathematical economics Control theory

Mathematics as profession

The best-known award in mathematics is the Fields Medal,[35][36] established in 1936 and now awarded every 4 years. It is often considered the equivalent of science's Nobel Prizes. The Wolf Prize in Mathematics, instituted in 1978, recognizes lifetime achievement, and another major international award, the Abel Prize, was introduced in 2003. The Chern Medal was introduced in 2010 to recognize lifetime achievement. These are awarded for a particular body of work, which may be innovation, or resolution of an outstanding problem in an established field.
A famous list of 23 open problems, called "Hilbert's problems", was compiled in 1900 by German mathematician David Hilbert. This list achieved great celebrity among mathematicians, and at least nine of the problems have now been solved. A new list of seven important problems, titled the "Millennium Prize Problems", was published in 2000. Solution of each of these problems carries a $1 million reward, and only one (the Riemann hypothesis) is duplicated in Hilbert's problems.

See also

Nuvola apps edu mathematics blue-p.svg Mathematics portal
Book:Mathematics
Books are collections of articles that can be downloaded or ordered in print.
Main article: Lists of mathematics topics

Notes

  1. ^ No likeness or description of Euclid's physical appearance made during his lifetime survived antiquity. Therefore, Euclid's depiction in works of art depends on the artist's imagination (see Euclid).
  2. ^ Steen, L.A. (April 29, 1988). The Science of Patterns Science, 240: 611–616. and summarized at Association for Supervision and Curriculum Development, ascd.org
  3. ^ Devlin, Keith, Mathematics: The Science of Patterns: The Search for Order in Life, Mind and the Universe (Scientific American Paperback Library) 1996, ISBN 978-0-7167-5047-5
  4. ^ Jourdain.
  5. ^ Peirce, p. 97.
  6. ^ a b Einstein, p. 28. The quote is Einstein's answer to the question: "how can it be that mathematics, being after all a product of human thought which is independent of experience, is so admirably appropriate to the objects of reality?" He, too, is concerned with The Unreasonable Effectiveness of Mathematics in the Natural Sciences.
  7. ^ Eves
  8. ^ Peterson
  9. ^ Both senses can be found in Plato. Liddell and Scott, s.voceμαθηματικός
  10. ^ The Oxford Dictionary of English Etymology, Oxford English Dictionary, sub "mathematics", "mathematic", "mathematics"
  11. ^ S. Dehaene; G. Dehaene-Lambertz; L. Cohen (Aug 1998). "Abstract representations of numbers in the animal and human brain". Trends in Neuroscience 21 (8): 355–361. doi:10.1016/S0166-2236(98)01263-6. 
  12. ^ See, for example, Raymond L. Wilder, Evolution of Mathematical Concepts; an Elementary Study, passim
  13. ^ Kline 1990, Chapter 1.
  14. ^ "A History of Greek Mathematics: From Thales to Euclid". Thomas Little Heath (1981). ISBN 0-486-24073-8
  15. ^ Sevryuk
  16. ^ Johnson, Gerald W.; Lapidus, Michel L. (2002). The Feynman Integral and Feynman's Operational Calculus. Oxford University Press. ISBN 0821824139. 
  17. ^ Eugene Wigner, 1960, "The Unreasonable Effectiveness of Mathematics in the Natural Sciences," Communications on Pure and Applied Mathematics 13(1): 1–14.
  18. ^ "Mathematics Subject Classification 2010" (PDF). http://www.ams.org/mathscinet/msc/pdfs/classification2010.pdf. Retrieved 2010-11-09. 
  19. ^ Hardy, G. H. (1940). A Mathematician's Apology. Cambridge University Press. ISBN 0521427061. 
  20. ^ Gold, Bonnie; Simons, Rogers A. (2008). Proof and Other Dilemmas: Mathematics and Philosophy. MAA. 
  21. ^ Aigner, Martin; Ziegler, Gunter M. (2001). Proofs from the Book. Springer. ISBN 3540404600. 
  22. ^ Earliest Uses of Various Mathematical Symbols (Contains many further references).
  23. ^ Kline, p. 140, on Diophantus; p.261, on Vieta.
  24. ^ See false proof for simple examples of what can go wrong in a formal proof. The history of the Four Color Theorem contains examples of false proofs accidentally accepted by other mathematicians at the time.
  25. ^ Ivars Peterson, The Mathematical Tourist, Freeman, 1988, ISBN 0-7167-1953-3. p. 4 "A few complain that the computer program can't be verified properly", (in reference to the Haken-Apple proof of the Four Color Theorem).
  26. ^ Patrick Suppes, Axiomatic Set Theory, Dover, 1972, ISBN 0-486-61630-4. p. 1, "Among the many branches of modern mathematics set theory occupies a unique place: with a few rare exceptions the entities which are studied and analyzed in mathematics may be regarded as certain particular sets or classes of objects."
  27. ^ Zeidler, Eberhard (2004). Oxford User's Guide to Mathematics. Oxford, UK: Oxford University Press. p. 1188. ISBN 0198507631. 
  28. ^ Waltershausen
  29. ^ Shasha, Dennis Elliot; Lazere, Cathy A. (1998). Out of Their Minds: The Lives and Discoveries of 15 Great Computer Scientists. Springer. p. 228. 
  30. ^ Popper 1995, p. 56
  31. ^ Ziman
  32. ^ Luke Howard Hodgkin & Luke Hodgkin, A History of Mathematics, Oxford University Press, 2005.
  33. ^ Clay Mathematics Institute, P=NP, claymath.org
  34. ^ Like other mathematical sciences such as physics and computer science, statistics is an autonomous discipline rather than a branch of applied mathematics. Like research physicists and computer scientists, research statisticians are mathematical scientists. Many statisticians have a degree in mathematics, and some statisticians are also mathematicians.
  35. ^ "The Fields Medal is now indisputably the best known and most influential award in mathematics." Monastyrsky
  36. ^ Riehm

References

External links

Find more about Mathematics on Wikipedia's sister projects:
Definitions from Wiktionary
Images and media from Commons
Learning resources from Wikiversity
News stories from Wikinews
Quotations from Wikiquote
Source texts from Wikisource
Textbooks from Wikibooks
Wikiversity
At Wikiversity you can learn more and teach others about Mathematics at:
Diposting oleh di

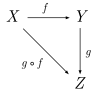
Tidak ada komentar:

Posting Komentar

Langganan: Posting Komentar (Atom)